Convergence and Ulam-Hyers-Rassias Stability Analyses of Numerical Solutions of Bratu Type Equations using Picard Method
Abstract
 Abstract Views: 0
Abstract Views: 0
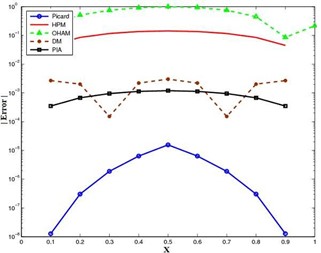
The Bratu equation is a basic nonlinear boundary value problem with important applications to fuel ignition, thermal combustion, and nanotechnology. The current article presents a new application of the Picard iterative technique to find accurate approximate solutions for this equation. Firstly, the conditions for existence and uniqueness of the solutions are determined. Furthermore, the article provides an explicit formulation of Picard’s scheme for second-order ordinary differential equations and its particular implementation to the Bratu type problem. The iterative solutions obtained are analyzed thoroughly for convergence and are proved to be Ulam-Hyers-Rassias stable, a very strong type of stability not yet known for these kind of solutions. Numerical tests for three cases ( , 2, and the critical value ) are shown to exemplify outstanding accuracy of the proposed approach. A thorough comparison with known techniques including the Adomian Decomposition Method, Homotopy Perturbation Method, and Variational Iteration Method indicates that the Picard iterative scheme is much better in terms of accuracy since its maximum absolute errors are much smaller
Downloads
References
Wang Y, Yu H, Tan F, Li S. Using an effective numerical method for solving a class of Lane-Emden equations. Abst Appl Anal. 2014; 2014: e735831. https://doi.org/10.1155/2014/735831
Chu Y. M, Ullah S, Ali M, Tuzzahrah G. F, Munir T. Numerical investigation of Volterra integral equations of second kind using optimal homotopy asymptotic method. Appl Math Comput. 2022; 430: e127304. https://doi.org/10.1016/j.amc.2022.127304
Saif Ullah, Amin F, Ali M. Numerical investigation with convergence and stability analyses of integro-differential equations of second kind. Int J Comput Meth. 2024; 21(3): e2350036.
https://doi.org/10.1142/S0219876223500362
Mohsin A. A simple solution of Bratu problem. Comput Math Appl. 2014; 67: 26-33. https://doi.org/10.1016/j.camwa.2013.11.004
Gelfand I. M. Some problems in the theory of quasi-linear equations. Transac Amer Math Soc. 1963; 29: 295-381.
https://doi.org/10.1090/S0002-9947-1963-0153125-6
Wan YQ, Guo Q, Pan N. Thermo electro hydrodynamic model for electrospinning process. Int J Nonlin Sci Numer Simul. 2004; 5(1): 5-8. https://doi.org/10.1515/IJNSNS.2004.5.1.5
Jacobsen J, Schmitt K. The Liouville-Bratu-Gelfand problem for radial operators. J Differ Equ. 2002; 184: 283-298.
https://doi.org/10.1006/jdeq.2001.4151
Kafri HQ, Khuri SA. A novel approach using fixed point iterations and Green’s functions. Comput Phy Commun. 2016; 198: 97-104.
https://doi.org/10.1016/j.cpc.2015.09.007
Abukhaled M, Khuri SA, Sayfy A. Spline-based numerical treatments of Bratu-type equations. Palestine J Math. 2012; 1: 63-70.
Boyd JP. Chebyshev polynomial expansions for simultaneous approximation of two branches of a function with application to the one-dimensional Bratu equation. Appl Math Comput. 2003; 142: 189-200. https://doi.org/10.1016/S0096-3003(02)00293-8
WazwazA M. Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl Math Comput. 2005; 166: 652-663.
https://doi.org/10.1016/j.amc.2004.06.059
Kashkari BSH, Abbas SZ. Solution of initial value problem of Bratu type equation using modifications of homotopy perturbation method. Int J Comput Appl. 2017; 162: 44-49.
https://doi.org/10.5120/ijca2017913377
Feng X, He Y, Meng Y. Application of homotopy perturbation method to the Bratu type problems. Topol Meth Nonlin Anal: J Juliusz Schauder Cent. 2008; 31: 243-252. https://doi.org/10.12775/TMNA.2008.015
Aksoy Y, Pakdemirli M. New perturbation iteration solutions for Bratu-type equations. Comput Math Appl. 2010; 59: 2802-2808.
https://doi.org/10.1016/j.camwa.2010.01.050
Darwish MA, Kashkari BS. Numerical solutions of second order initial value problems of Bratu type via optimal homotopy asymptotic method. Am J Comput Math. 2014; 4: 47-54.
https://doi.org/10.4236/ajcm.2014.41004
Khuri SA. A new approach to Bratu’s problem. Appl Math Comput. 2004; 147: 131-136. https://doi.org/10.1016/S0096-3003(02)00655-2
Batiha B. Numerical solutions of Bratu type equations by the variational iteration method. Hacett J Math Statis. 2010; 391: 23-29.
Salem SA, Thanoon TY. On solving Bratu’s type equation by perturbation method. Int J Nonlin Anal Appl. 2022; 13(1): 2755-2763. https://doi.org/10.22075/IJNAA.2022.5983
Caglar H, Caglar N, Ozer M, Valaristos A, Anagnostopoulos AN. B Spline method for solving Bratu’s problem. Int J Comput Math. 2010; 87(8): 1885-1891. https://doi.org/10.1080/00207160802450136
Gutierrez JM, Veron MAH. A picard-type iterative scheme for Fredholm integral equations of the second kind. Mathematics. 2021; 9(1): 1-15. https://doi.org/10.3390/math9010087
Robin W. Iterative solutions to classical second-order ordinary differential equations. J Innov Technol Edu. 2019; 6: 1-12. https://doi.org/10.69437/jite.6.1_1
Rahman M. Integral Equations and their Applications. Southhampton: WIT Press; 2007.
Wang Y, Ni G, Liu Y. Multi step Newton-Picard method for nonlinear differential equations. J Guid Cont Dynam. 2020; 43(11): 2148-2155. https://doi.org/10.2514/1.G005249
Yang AM, Zhang C, Jafari H, Cattani C, Jiao Y. Picard successive approximation method for solving differential equations arising in fractal heat transfer with local fractional derivative. Abstract Appl Anal. 2014; 2014: e395710. https://doi.org/10.1155/2014/395710
Ulam S. M. A Collection Mathematical Problems. Interscience; 1960.
Hyers D, H. On the stability of the linear functional equation. Proc Natl Acad Sci. 1941; 27(4): 222-224. https://doi.org/10.1073/pnas.27.4.222
Zhao K. Generalized UH-stability of a nonlinear fractional coupling (p1, p2)-Laplacian system concerned with nonsingular Atangana- Baleanu fractional calculus. J Inequal Appl. 2023; 2023: e100. https://doi.org/10.1186/s13660-023-03009-w
Zhao K. Solvability and GUH-stability of a nonlinear CF-fractional coupled Laplacian equations. AIMS Mathematics. 2023; 8(6): 13351-13367. https://doi.org/10.3934/math.2023673
Zada A, Faisal S, Li Y. Hyers-Ulam-Rassias stability of nonlinear delay differential equations. J Nonl Sci Appl. 2017; 10: 504-510.
https://doi.org/10.22436/jnsa.010.02.08
Huang J, Jung S. M, Li Y. On Hyers-Ulam stability of nonlinear differential equations. Bull Korean Math Soc. 2015; 52: 685-697.
https://doi.org/10.4134/BKMS.2015.52.2.685
Qarawani MN. Hyers-Ulam-Rassias stability criteria of nonlinear differential equations of Lane-Emden type. Gen Lett Math. 2017; 3(1): 57-70. https://doi.org/10.31559/glm2017.3.1.6
Wang X, Luo D, Zhu Q. Ulam-Hyers stability of Caputo type fuzzy fractional differential equations with time-delays. Chaos Solit Fract. 2022; 156: e111822. https://doi.org/10.1016/j.chaos.2022.111822
Luo D, Wang X, Caraballo T, Zhu Q, Ulam-Hyers stability of Caputo-type fractional fuzzy stochastic differential equations with delay. Commun. Nonlin Sci Numer Simul. 2023; 121: e107229.
https://doi.org/10.1016/j.cnsns.2023.107229
Wazwaz AM. A First Course in Integarl Equations. World Scientific Publishing Company; 2015.
Reddy BD. Introductory Functional Analysis With Application to Boundary Value Problems And Finite Elements. Springer Verlag Incorporation; 1998.
Copyright (c) 2025 Saif Ullah, Muzaher Ali, Sana Bajwa, Ahsan Bilal

This work is licensed under a Creative Commons Attribution 4.0 International License.





